Frequency Analysis...

Frequency Analysis Diagram
Originally uploaded by Astro Guy

The first process usually done on the time series of a variable star is the frequency analysis. For a star with periods on the order of a day, such as with gamma Doradus types, ground based data can be quite troublesome to work with due to aliasing. The aliasing comes from the day-night cycle of the Earth where a star can only be observed at night. With a spacebased telescope in a proper orbit this problem disappears.

For HR 1613 we obtained 8.5 days of data that is nearly continuous. The result is that we can resolve individual frequencies that compose the lightcurve shape. Mathematically, we want to fit a function consisting of sine curves that have different frequencies, amplitudes and phases. Fitting an equation of this form in a non-linear problem. This means that finding a set of parameters that best fits the data is tricky business.

One method of estimating the best fit parameters is to use a Fourier Transform (in this case, discrete=DFT) to estimate parameters. The method is simple to describe:

1. Perform the DFT of dataset
2. Record the frequency and phase with the highest amplitude
3. use DFT info as guess for fit solution. Then optimize solution.
4. remove solution from original data set to produce residuals.
5. Perform DFT on residuals.
6. Find next highest amplitude.
7. add new frequency to solution and optimize again.
8. repeat 4-7 until there are no significant frequencies remaining in the DFT.

There are some hiccups along the way. The above method does not guarantee that you have found the best solution. Also, your solution parameters may become degenerate if two frequencies are inserted in the solution that are seperated less than the resolution afforded by your observations.

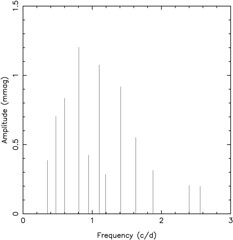
The best way around resolution problems, is to gather more observations! Otherwise, one must be quite careful about claims one may make based on a non-linear model as you may not have found the best solution. The Figure above shows a solution for HR 1613. So far I am not convinced that is a unique solution and it will be very difficult to get new observations. So I'm working on methods to test the uniqueness by efficiently exploring the local parameter space for the model parameters to find other local-minimum/maximum.